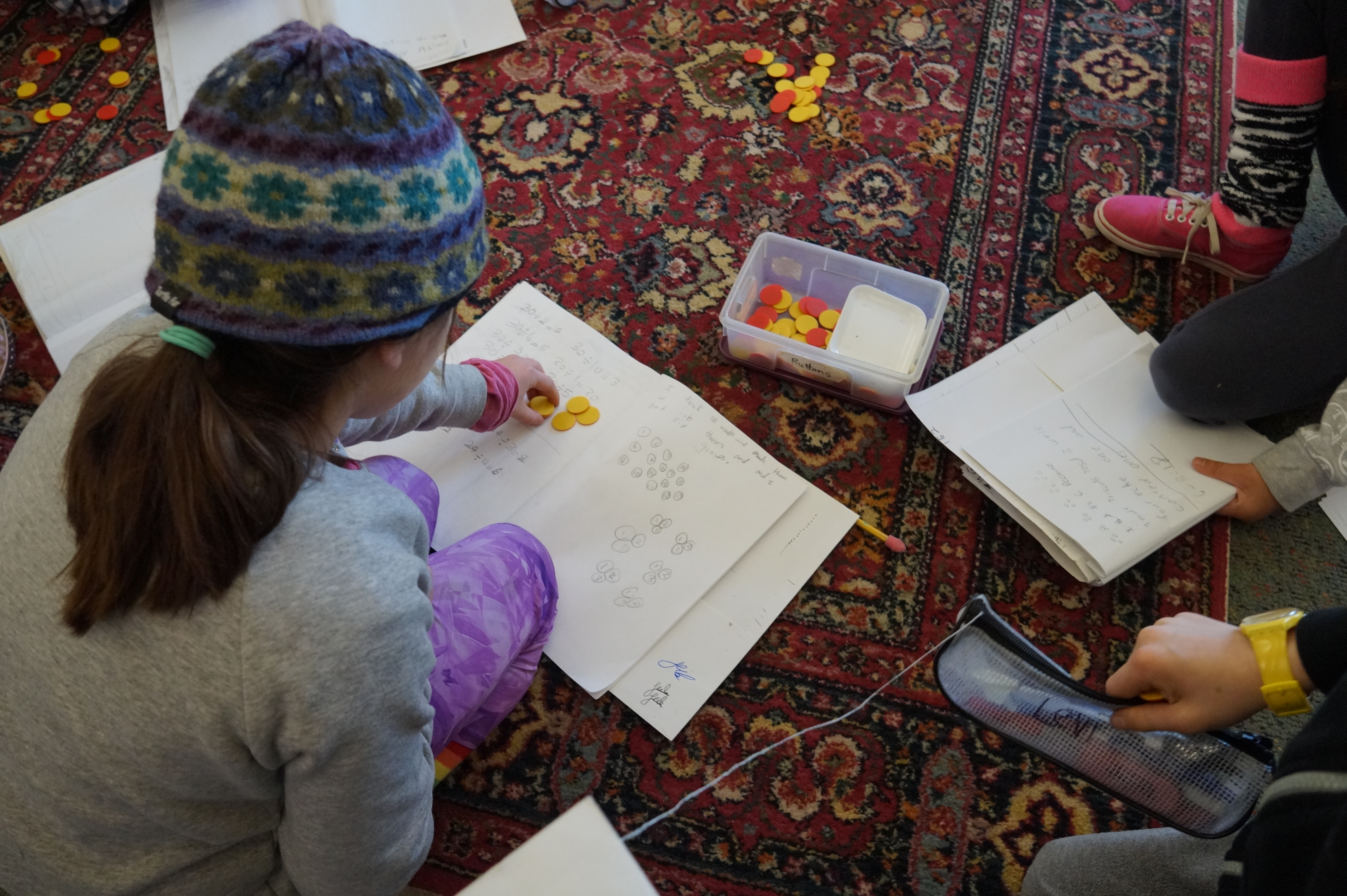Mathematics
The overall goal of mathematics learning at Miquon is to enable children to understand and apply mathematics throughout their lives. We want them to become confident mathematical thinkers who understand why as well as how and who can see connections and continuity in their growing mathematical knowledge. Our approach to mathematics instruction is based on inquiry, discovery, reasoning, and application across curriculum areas. We want children to be makers and builders of their own mathematical understanding, not passive receivers of rules and procedures. We want them to view mathematics as an area for play and recreation as well as a set of useful skills.
Approach
Abstract concepts and real-world applications exist together in our children’s experience. Our students do mathematics with their hands as well as their heads throughout their years at Miquon. They build, measure, weigh, count, design, cook, sort, and arrange. A kindergarten group may do mathematics for weeks that is focused on the baskets of apples they have brought back from an orchard. Third and fourth graders may play dice games that let them discover basic probability concepts as well as have lots of practice with addition and subtraction. Our fifth and sixth graders may build toothpick bridges in a project that requires them to work within a budget, create 2D scale drawings of their 3D ideas, and discover the stability of triangles. Tools and technology are embedded in many activities: computer software, calculators, rulers, compasses, protractors, scales, our classroom kitchens, and our workbenches are all involved in mathematics instruction. Communication is an essential component of our program, and students are expected to justify their ideas, listen to classmates’ alternative strategies, and build the vocabulary.
One reason is that it encourages inquiry and problem-solving. When students need what they are learning, they are more likely to value and retain new skills and concepts. When they recall prior activities and similar projects, they can construct new uses for old skills and extend their understanding. Games and puzzles that involve mathematics bring fun and excitement into what could otherwise be a dry lesson. Another reason is that our program is flexible. It is based on close observation of students as they work and is adjusted to accommodate a child’s readiness, learning style, pace, and need for more challenge or more explicit instruction. No two learners are alike, and no single plan fits everyone. As a result, our students go on to their next schools and into their adult lives believing in themselves as mathematicians, seeing mathematics as something for which they have daily use, and having a strong conceptual understanding on which to build new knowledge.
Scope and Sequence
Our mathematics program is based on Focal Points from the National Council of Teachers of Mathematics. It is implemented through the use of many different published materials (such as Math in Focus, Investigations, and IMP), teacher-created materials, games, and projects. In keeping with the recommendations from NCTM, we constantly strive to provide “contexts that promote problem solving, reasoning, communication, making connections, and designing and analyzing representations.” One of the ways we do that is by integrating mathematics instruction and applications into other parts of our students’ day, including art, music, science, and social studies.
View the Math Curriculum Scope and Sequence.
Essential Questions
- What do we mean by mathematics?
- Does it always involve numbers or does it take other forms, too?
- How have cultures and individuals helped to create the math we use today?
- Is mathematics a collection of inventions or discoveries or both?
- How can we use mathematics to describe and understand the physical world?
- Are there mathematical ideas that are imaginary?
Attitudes, Assumptions, and Habits of Mind
- Everyone needs and can learn to use mathematics.
- Communication is an important part of mathematics.
- Mathematics is often used to persuade, so we must become wise evaluators of data and statistics.
- All mathematical ideas are founded on a chain of reasoning.
- We can convey and justify our ideas in many different ways.
- Inquiry and flexibility are important parts of mathematical thinking.
- Mathematics is a living science that is continuing to grow and change.
- Mathematics can be a form of recreation as well as a practical tool.