Visualizing for Understanding
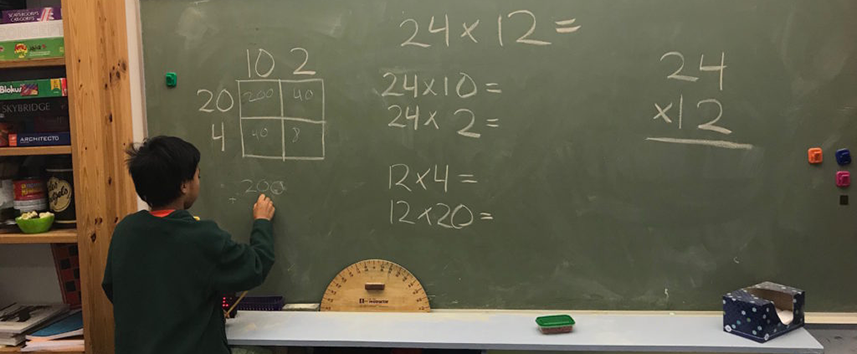
Understanding mathematical operations is about seeing and understanding how and why they work, not about taking someone’s word for it (a teacher’s, a friend’s, or a textbook’s). While all of that input can be helpful, there is nothing like making the discovery for yourself — constructing your own understanding — for making a concept stick and be easily transferred to other situations.
In the pictures above, one student is at the board making the connection between a box visualization of multiplication, the partial products that are involved, and the standard (or traditional) algorithm.
In the other two photos, a small group wrestles with the nature of division, finding out for themselves why a “remainder,” a term with which they are very familiar is, in fact, a fraction! It took some doing — including setting up a trading station for Dienes blocks (base-ten blocks), but every child in the group seemed to have their own “a-ha!” moment. Ask your child what “a-ha” moment they’ve had lately, in math or anything else. And perhaps share one of your own!
